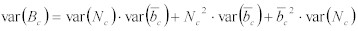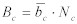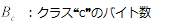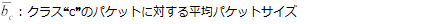パケットサンプリングの基礎
(Packet Sampling Basics)
はじめに
パケットサンプリングについては、収集されたデータから推定値を導き出す手法とその理論については、InMon社が、sFlow.orgにてパケットサンプリングの基礎 (Packet Sampling Basics)として提示しているので、それを参照いただきたい。
ここでは、それを翻訳していますが、理論的に難解なこともあり、正確な翻訳ができていません。
正確な情報は、原本となる、
Packet Sampling Basics( http://www.sflow.org/packetSamplingBasics/index.htm )を参照いただきたいと考えます。
ただ、会社方針の代表メッセージにも書きましたが、サンプリングについては、「低価格・低負荷で広範なネットワークトラフィックの分析を可能にするという意味」で、有益なものと考えており、それを理論づける背景として、下に説明している内容をベースにしていただきたいと思います。
概要
パケットベースのサンプリング処理は、広くネットワークトラフィックの特性を示すと言える。パケットサンプリングは、トラフィック内の定期的なパターンと同期させないために、サンプリングプロセス内でランダムに実行される。通常、Nパケット分の1の割合でパケットをキャプチャーし、分析するという指定を行う。
このようなパケットサンプリングは、100%正確な結果は提供できないが、結果に対して、その定量的な正確さを提示することは可能である。このドキュメントでは、パケットサンプリング処理プロセスでの、そのいくつかの例の提示と結果の計算方法や定量的な正確さの提示方法の基本的技術の説明を行う。
実例
ネットワーク内に、1,000,000パケット流れたと仮定する。そして、0.25%のサンプリングレートでサンプルパケットを取得する(2,500パケットを取得)。もし、サンプルパケットの内、1,000パケットがトラフィック内のあるクラスのパケットであった場合、たとえば、Voiceトラフィックだった場合、1,000,000パケットの内、正確に何パケットがVoiceパケットだっただろうか? 少なくとも、1,000パケットはVoiceパケットだったと判断できる。なぜなら、それらはサンプル内に含まれていたからである。考えられるVoiceパケットの最大数は、998,500パケットである。なぜなら、サンプルされたパケットの内、1,500パケットは、Voiceパケット以外のものと確認されているからである。しかし、これら2つの値は、ともに有り得そうに無い値である。Voiceトラフィックの割合は、サンプル内に見られるVoiceトラフィックの割合(40%:1,000を2,500で割った値)と同じと考えるのが、最もありえそうな値と言える。このことから、Voiceパケット総数の最適な推定値は、400,000フレームと言う事が出来る。
概して、パケット総数 ❝N❞、サンプルパケット総数 ❝n❞、クラス別のサンプル数 ❝c❞ を用いてクラス別のフレーム数 ❝Nc❞ を、以下の方程式で推測する事が出来る。
Equation 1:
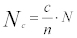
もちろん、正確にVoiceパケットが、400,000パケットだったとは、考えにくい。その為、実際の値が含まれる可能性(95%の可能性とする)がある小さい範囲の値を明示することができる。そうであれば、上のケースでは、実際のVoiceの数が、381,000パケットから419,000パケットだった可能性が95%あると推定することができる。
以下の方程式により、❝Nc❞の推定値の分散が計算される。:
Equation 2:
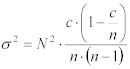
❝Nc❞に対する95%信頼区間は、以下のようになる。:
Equation 3:
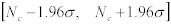
ここで表現された範囲を、分かりやすくパーセントで表現すると、❝400,000+/-4.8%パケットが送出された❞ あるいは、❝最大誤差が4.8%である❞と言うことが出来る。
以下の方程式により、誤差のパーセンテージを簡略化して提示することができる。:
Equation 4:
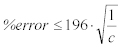
この方程式を以下のチャートのようにプロットすると、❝c❞ が大きくなると正確さが向上することが確認できる。
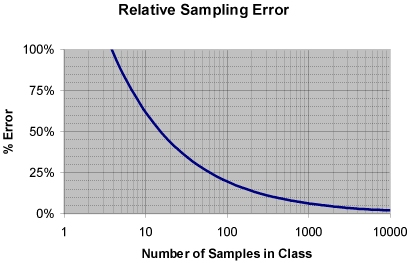
Chart 1: サンプリング数と誤差との関連
例として、❝c❞ が1,000の時の誤差のパーセンテージを確認すると、概ね、❝6%❞と読み取ることが出来る。
注意すべき興味深い点は、測定の正確さは、フロー内の総フレーム数に依存するのではなく、実際に推定に使われるのは、サンプル数だけという事である。この事は、ハイスピードなスイッチやルーターをモニタリングする場合、有益という事ができる。例えば、平均400フレーム/秒流れる小さなスイッチをサンプリングレート0.25%でモニタリングできると仮定すると、平均40,000フレーム/秒流れるファースト・スイッチを同じレベルの正確さでモニタリングする場合、たった0.0025%のサンプリングレートで可能になるということである。
統計サンプリングは、測定間隔が短い時やトラフィック・レートが非常に低い時、真の値に対して著しく幅のある範囲で推定結果を算出する。これを以下に例をもって示す。
フローが1秒間に1パケット送出するVoiceトラフィックを含んでいると仮定し、それを1時間モニターした場合、Voiceパケットは、1時間に3,600パケットあるという事になる。もし、サンプリング・レートが0.25%に設定されていた場合、概ね9パケットのVoiceパケットがサンプリングされると考えられる。この場合、誤差のパーセンテージは、65%にもなってしまう。これは、一時間でのVoiceパケットの推定値が、1,200パケットから6,000パケットの範囲で推定されることを意味する。
正確さを向上させるには、2つの方法が考えられる。一つ目は、サンプリング・レートを上げてやることである。上の例で、サンプリング・レートを1%に上げた場合、概ね1時間に36パケットのVoiceパケットがサンプリングされると考えられ、誤差のパーセンテージは、33%となるので、一時間でのVoiceパケットの推定値も2,400パケットから4,800パケットとより狭い範囲で推定されることとなる。ただ、この場合、ネットワーク上のサンプルトラフィック量やサンプルを分析するための処理量も増加することにも注意しなければならない。
正確さを向上させるもうひとつの方法は、長期間のサンプルデータから推定することである。
月次分析を当初の0.25%のサンプリング・レートで行った場合、上の例では、一か月で6,700パケットのVoiceパケットがサンプリングされると考えられ、誤差のパーセンテージは、たった2.4%となるので、一か月でのVoiceパケットの推定値も2,610,000パケットから2,740,000パケットの範囲で推定出来ることになる。このように、さらに正確な情報を要求されるネットワークの使用内容によるビリング(課金)などに使用する場合は、週次や月次のような長期間での分析が望ましい。
ほとんどの場合、このサンプリング処理によって、適切な値を推定することが出来る。特に、大きなトラフィック・ソースでは、短い間隔でも、効果的にリアルタイムでの輻輳管理を行うのに十分正確な推定を行うことが出来る。また、使用内容に対するビリング(課金)やキャパシティー・プランニングのように、さらなる正確性を要求される場合は、長期間でのデータを対象とするなど、適切な正確度に合致するよう運用しなければならない。
セオリー
パケットサンプリングは、二項分布に従うと考えられる。
二項分布は、変数 ❝c❞の性質を表現する。もし、以下の条件と合致する場合、
1. 測定数❝n❞が固定
2. それぞれの測定が、独立している
3. それぞれの測定は、2つの結果のひとつとして表現される(”成功”or”失敗”)
4. ”成功”の確立❝p❞は、それぞれの測定で同じである
❝c❞は、パラメーター❝n❞と❝p❞を用いて二項分布となる。
以下は、二項分布における平均と分散の計算式を示す。:
Equation 5:
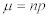
Equation 6:
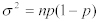
パケットサンプリングに対しては、母比率(サンプルが実際のクラスに属する確率❝p❞)が未知であるが、標本比率(”成功数”を、測定数で割ったもの)に関しては算出可能である。:
Equation 7:
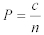
P = 標本比率
c = 与えられたクラス(”成功”)のサンプル数
n = サンプル数
Jedwab et. al.( HPL-92-35.pdf )は、条件4が、いくつかのランダムパケットサンプリングに対して有効であると証明している。このように、測定数❝n❞、”成功”数❝c❞、成功確率❝p❞により二項分布に従うならば、標本比率❝P❞の分布についての情報を導き出すことが出来る。
平均値に対する掛け算の特性によって、分布❝P❞の平均値は、分布❝c❞を❝n❞で割った分布の平均値となる。ゆえに、:
Equation 8:
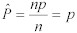
このように、標本比率❝P❞は、母比率❝p❞の不偏推定量となる。
❝P❞の分散は、❝c❞を❝n❞で割った分散と等しくなる。また、定数により乗算された乱数の分散は、以下の方程式に従う。:
Equation 9:
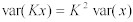
従って:
Equation 10:
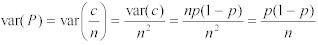
サンプル数❝n❞が十分大きいとき、標本比率は、中心極限定理(Central Limit Theorem)によって、期待値❝p❞と分散❝p(1-p)/n❞により、正規分布に近似する。
これらの推定を使用し、❝p(母比率)❞の最大尤度推定量は、標本比率❝P❞となる。そして、標本比率の分散は、母比率の分散の不偏推定量となる。:
Equation 11:
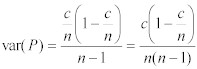
Note: 除数は、❝n❞より❝(n-1)❞が適切である。なぜなら、❝n❞は、確率(既知の分布)で適切であり、❝(n-1)❞は、統計値(未知の分布)で有効であるからである。
(自由度の説明)
一方、クラス別のフレーム総数の推定値❝Nc❞を考える場合:
Equation 12:
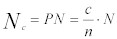
N は、フレーム総数
そこで、推定値❝Nc❞の分散は、以下のように表現できる:
Equation 13:
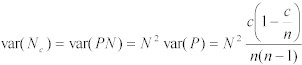
❝Nc❞の95%信頼区間は、以下である。:
Equation 14:
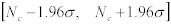
ここで表現された範囲を、分かりやすくパーセントで表現すると、以下のようになる。:
Equation 15:
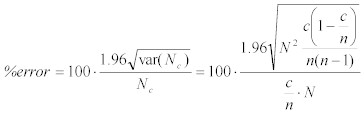
これを展開すると、:
Equation 16:
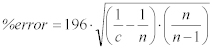
一般的に、❝n >> c❞が成立するので、これを方程式に適用すると、以下のように簡略化される。:
Equation 17:
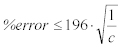
いままでのすべての方程式は、パケットカウントの推定を処理していた。もちろん、個々のクラス別に集約されたバイト数を推定するのに有効である。バイト数の推定に関しては、以下の方程式により計算される。:
Equation 18:
平均パケットサイズとパケットサイズの分散は、以下の方程式により計算される。:
Equation 19:
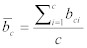
そして、
Equation 20:
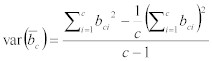
二つの乱数を掛ける場合、その結果の分散は、以下の方程式で導き出せる。:
Equation 21:
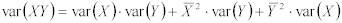
この方程式を、Bcに適用すると、以下のようになる。:
Equation 22: